Bobi este un excursionist pasionat. Zona muntoasă pe care o va vizita în această vară are o caracteristică atractivă: există un sistem de transport cu telecabina. Proiecţia pe un plan orizontal a traseului ales de Bobi este o linie dreaptă. Anumite puncte situate pe munte, dintre care unele se află pe traseul telecabinei, se numesc cote. Proiecţiile cotelor pe orizontală sunt puncte coliniare aflate unul faţă de altul la distanţa de un kilometru.
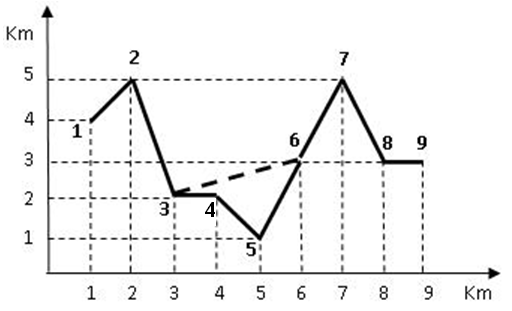 In figură, cu linie plină este reprezentat profilul muntelui, iar cu linie punctată îngroşată traseul telecabinei, acolo unde acesta nu coincide cu profilul muntelui. Telecabina parcurge segmentele care unesc cotele: şi .
In figură, cu linie plină este reprezentat profilul muntelui, iar cu linie punctată îngroşată traseul telecabinei, acolo unde acesta nu coincide cu profilul muntelui. Telecabina parcurge segmentele care unesc cotele: şi .
Fie înălţimile cotelor. Viteza normală cu care se deplasează telecabina este de Km / oră. Traseul telecabinei este formată din segmente de dreaptă şi urmează în general profilul muntelui, trecând prin fiecare cotă. Abaterea traseului telecabinei de la profilul muntelui are loc în situaţia în care un cablu de telecabină poate fi întins direct între o cotă şi prima cotă , aflată în direcţia de deplasare, care se află la o înălţime mai mare decât cota .
Bobi dispune de suma de euro. Pentru fiecare segment de drum parcurs între două cote şi , el trebuie să plătească suma euro dacă este vorba de o porţiune de urcare în pantă şi nu trebuie să plătească nimic dacă este vorba despre o porţiune orizontală.
La coborârea unei pante situată între două cote şi Bobi are două variante: prima variantă este de a coborî cu viteza normală Km/oră şi atunci nu plăteşte nimic. A doua variantă, pe care băiatul o poate alege prin apăsarea unui buton în telecabină, este de a coborî panta, indiferent de lungimea ei, în timpul de o oră, deci cu o viteză diferită de cea normală, dar în acest caz Bobi trebuie să plătească suma euro.
Cerinţă
Cunoscând înălţimile celor n cote prin care va trece telecabina şi suma de care dispune Bobi, scrieţi un program care determină:
- lungimea totală a traseului telecabinei măsurat între cota şi cota .
- timpul minim exprimat în ore de care are nevoie Bobi ca să ajungă la o cotă de pe drum cu numărul de ordine mai mare sau egal cu dat, ştiind că porneşte de la cota şi că există cel puţin o variantă care conduce la acest timp minim şi care necesită o sumă mai mică sau egală cu .
Date de intrare
Fişierul de intrare telecab.in conţine pe prima linie trei numere naturale separate prin câte un spaţiu.
Pe fiecare dintre următoarele linii se găseşte câte un număr natural. Pe linia se găseşte numărul , exprimat în kilometri, reprezentând înălţimea cotei .
Date de ieșire
Fişierul de ieşire telecab.out va conţine pe prima linie un număr întreg , reprezentând lungimea totală a traseului telecabinei, între cotele şi , exprimat în kilometri. Pe linia a doua se va scrie numărul natural , reprezentând timpul minim de care are nevoie Bobi ca să atingă o cotă având numărul de ordine mai mare sau egal cu .
Restricții și precizări
- distanţa dintre două cote succesive de pe traseu se calculează ca fiind partea întreagă a distanţei euclidiene în plan dintre cele două cote.
- între două cote consecutive, profilul muntelui este un segment de dreaptă care uneşte cotele.
- pentru toate cazurile de test se garantează că Bobi are suficienţi bani pentru a atinge sau a depăşi cota K.
- pentru mişcarea rectilinie cu viteza constantă, distanţa = viteza × timpul.
- pentru rezolvarea primei cerinţe se obţine din punctajul fiecărui test
Exemplul 1
telecab.in
9 8 7
4
5
2
2
1
3
5
3
3
telecab.out
12
9
Explicație
Exemplul este cel din figură. Lungimea traseului telecabinei este:
Timpul minim de deplasare până la cota este:
Segmentul se parcurge în ore şi se cheltuie euro.
Segmentul se parcurge în ore şi se cheltuie euro.
Segmentul se parcurge în ore şi se cheltuie euro.
(distanţa de la cota la cota este: , iar timpul este ).
Segmentul se parcurge în ore şi se cheltuie euro.
Segmentul se parcurge în ore şi se cheltuie euro.
Exemplul 2
telecab.in
5 3 2
1
2
2
3
1
telecab.out
5
3
Explicație
Lungimea traseului telecabinei este:
Timpul minim de deplasare până la cota este:
Segmentul se parcurge în ore şi se cheltuie euro.
Segmentul se parcurge în ore şi se cheltuie euro.
Se observă că telecabina atinge cotele şi , trecând pe deasupra cotei .