Tsubasa-chan adoră dulciurile! De curând a apărut un nou tip de desert. Astfel decide să înfăptuiască o nouă fabrică care să producă acest produs delicios.

Fabrica conține un container imens pătratic, plin de aluat, de $10^6 × 10^6$ unități. Fiecare punct din container are drept coordonate o pereche de numere reale (x, y), unde $0 ≤ x, y ≤ 10^6$, iar fiecare punct are o dulceață. Dulceața unui punct este un număr real, inițial 0. Pentru fabricarea desertului este nevoie de Q operații, care pot fi de următoarele tipuri:

• O îndulcire verticală, determinată de o coordonată $x_u$ întreagă și o valoare întreagă v. După această operație, toate punctele din container (x, y) unde $x_u ≤ x < x_u + 1$ devin mai dulci cu v.
• O îndulcire orizontală, determinată de o coordonată $y_u$ întreagă și o valoare întreagă v. După această operație, toate punctele din container (x, y) unde $y_u ≤ y < y_u + 1$ devin mai dulci cu v.
• O degustare, determinată de 4 coordonate întregi $x_q, y_q, x^′_q, y^′_q$. Pentru această operație, Tsubasa ia o lingură, o pune în aluat la punctul $(x_q, y_q)$, și apoi o duce in linie dreaptă la punctul $(x^′_q, y^′_q)$. Mișcarea se efectuează într-o secundă, cu viteză constantă. După aceea, Tsubasa gustă desertul, vrând să afle dulceața totală a aluatului din lingură. Această valoare se calculează în felul următor: dacă lingura trece prin zone de dulceață $d_1$ pentru $t_1$ secunde, de dulceață $d_2$ pentru $t_2$ secunde, $\ldots$ , și de dulceață $d_k$ pentru $t_k$ secunde, atunci dulceața totală din lingură este $t_1d_1 + t_2d_2 + \ldots + t_kd_k$. Nu se modifică dulceața din container.

Cerință

Dându-se toate operațiile întreprinse în producerea desertului, să se găsească dulcețile totale ce sunt găsite la toate operațiile de degustare.

Date de intrare

Pe prima linie a fișierului de intrare dulciuri.in se va găsi numărul Q de operații.
Pe următoarele Q linii urmează descrieri a tuturor operațiilor, câte una pe linie, în ordine. O operație este codificată în felul următor:

• O îndulcire verticală este codificată prin $1 \; x_u \; v$.
• O îndulcire orizontală este codificată prin $2 \; y_u \; v$.
• O degustare este codificată prin $3 \; x_q \; y_q \; x^′_q \; y^′_q$.

Date de ieșire

În fișierul de ieșire dulciuri.out, să se afișeze toate rezultatele degustărilor, în ordine, câte una pe linie. Rezultatul unei degustări se consideră a fi corect daca eroarea absolută sau relativă față de soluția comisiei este cel mult $10^{−7}$. Dacă soluțiile comisiei și a concurentului sunt $s^∗, s$ atunci eroarea absolută este $|s^*−s|$ și eroarea relativă este $|s^*−s|/|s^*|$

Restricții

• Toate coordonatele din datele de intrare sunt întregi în intervalul $[0, 10^6]$.
• 0 ≤ v ≤ 1 000.
• v este întreg.
• 1 ≤ Q ≤ 100 000.
• Pentru 20 de puncte: Nu se fac îndulciri orizontale. Q ≤ 2 000.
• pentru alte 20 de puncte: Pentru fiecare degustare, fie $x_q = x^′_q$ sau $y_q = y^′_q$. Q ≤ 2 000
• Pentru alte 10 puncte: Se face cel mult o degustare
• pentru alte 20 de puncte: Toate degustările se fac după toate îndulcirile
• Pentru alte 10 puncte: Q ≤ 2 000
• pentru alte 20 de puncte: Fără restricții suplimentare

Exemple

dulciuri.in

3
1 2 60
2 3 60
3 0 0 3 4

dulciuri.out

35

dulciuri.in

4
1 2 10
3 2 0 2 1
3 3 0 3 1
3 2 0 2 0

dulciuri.out

10
0
10

dulciuri.in

6
1 4 413
1 3 234
2 5 244
2 3 777
3 1 2 14 15
3 31 4 2 40

dulciuri.out

128.3076923077
29.0881226054

Explicație

Situația pentru degustarea din primul exemplu este explicată în diagrama de mai jos.

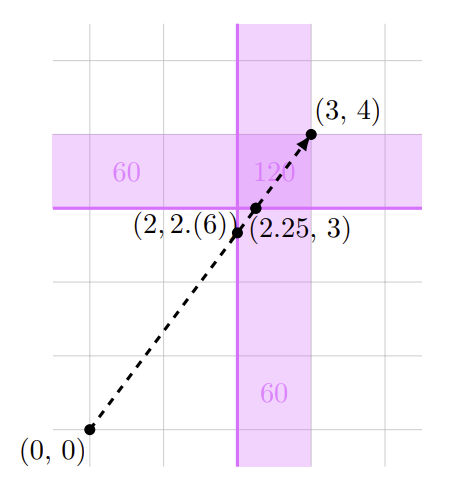
Zonele roz sunt zonele în care s-a aplicat o îndulcire, și numerele reprezintă cu cât s-a îndulcit. Zona din intersecția îndulcirilor are dulceața 120. Linia diagonală punctată reprezintă traseul.
Traseul are lungimea $\sqrt{3^2+4^2}=5$, și este completat într-o secunda — astfel are viteza de 5 unități pe secundă. Segmentul de la (2, 2.(6)) la (2.25, 3) are lungimea $\sqrt{(2.25 − 2)^2 + (2.(6) − 3)^2} = \sqrt{(1/4)^2 + (1/3)^2} = 5/12$, și are dulceața 60 — astfel el este traversat în (5/12)×(1/5) = 1/12 secunde, și contribuie cu (1/12)×60 = 5 la dulceața totală. Segmentul de la (2.25, 3) la (3, 4) are lungimea $\sqrt{(3 − 2.25)^2 + (4 − 3)^2} = 5/4$, și are dulceața 120 — astfel el este traversat în (5/4) × (1/5) = 1/4 secunde, și contribuie cu (1/4) × 120 = 30 la dulceața totală. Astfel, cum segmentul de la (0, 0) la (2, 2.(6)) contribuie cu 0, dulceața totală este 35.

Situația pentru degustările din al doilea exemplu este explicată în diagrama de mai jos.

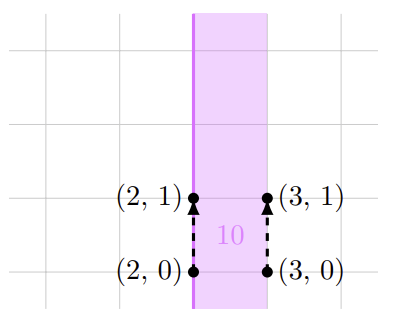
În primul traseu (cel din stânga) trecem mereu printr-o zonă cu dulceața 10, deci rezultatul degustării este 10. În al doilea traseu (cel din dreapta) trecem mereu printr-o zonă cu dulceața 0, deci rezultatul degustării este 0. În al treilea traseu, stăm pe loc pentru o secundă într-o zona de dulceață 10, deci răspunsul este 10