Judeţul în care are loc Olimpiada Naţională de Informatică de anul acesta este puţin ciudat. În judeţ există N oraşe, numerotate de la 1 la N. Fiecare dintre cele N oraşe ale judeţului este legat de EXACT alte 2 oraşe, prin străzi bidirecţionale. Şi mai ciudat este faptul că, în cadrul acestui sistem stradal, nu este întotdeauna posibil să ajungi din orice oraş în oricare alt oraş mergând pe străzi. Oricum, locuitorii judeţului sunt mândri de acest sistem al lor şi sunt de părere că nu mai există altul la fel. Dumneavoastră vreţi să le demonstraţi contrariul şi pentru aceasta vreţi să calculaţi câte sisteme stradale distincte cu proprietatea de mai sus există. Două sisteme sunt considerate distincte dacă există cel puţin o stradă între o pereche de oraşe i şi j în cadrul primului sistem, care nu există în cadrul celui de-al doilea.
Cerinţă
Scrieţi un program care să calculeze câte sisteme stradale distincte există modulo 1 000 000 007.
Date de intrare
Din fişierul sistem.in veţi citi valoarea întreagă n, reprezentând numărul de oraşe ale judeţului.
Date de ieşire
În fişierul sistem.out veţi afişa o valoare întreagă, reprezentând numărul de sisteme stradale distincte, cu proprietatea că orice oraş este legat prin străzi directe de exact alte 2 oraşe.
Restricţii
3 ≤ n ≤ 100 000- Restricțiile și cerința au fost modificate
- Pentru 16 puncte avem
n ≤ 14 - Pentru alte 16 puncte avem
n ≤ 100 - Pentru alte 16 puncte avem
n ≤ 500 - Pentru alte 16 puncte avem
n ≤ 2000
Exemple
sistem.in
4
sistem.out
3
sistem.in
6
sistem.out
70
sistem.in
776
sistem.out
552369242
Explicații
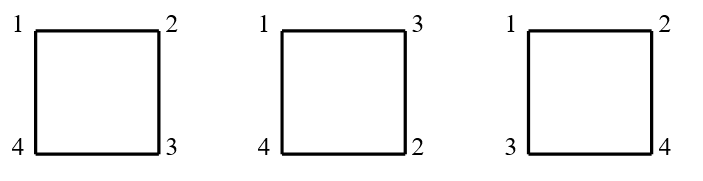
Cele 3 soluţii sunt următoarele: